Multiverse 2.357

Current “NISQ” quantum computers often produce errors when measurements are taken or gating operations are applied, and it is very costly in every sense of the term to deal with them. The ‘N’ in NISQ refers to “noisy; a reference to the fact that they are not capable of error correction.

High error rates are costly because you cannot copy a qubit during critical steps in the computational process. High error rates are also costly because error correction involves either redundancy in systems where there is a premium on qubits to begin with, or sending and receiving signals to and from the control systems into and out of the quantum processor hardware. Keep in mind also that these computations are often run thousands of times to give decisive results since those results are probabilistic in nature, and high error rates tend to increase the number of times these are run.

Error correction involves sending signals out to be evaluated to see if an error occurred. Then a corrective action is chosen and the signals needed to compensate are sent back in. All this needs to be timed appropriately so the computation can complete before the qubits decohere. Error correction is a bitch.

Detecting errors begins with measuring the values of parity qubits. The process of measuring can also be error-prone however, and these operations can actually introduce errors. The gating operations required to correct errors is similarly error-prone. So overall, error detection and correction schemes can in fact introduce more errors than they fix.

In spite of that, we need error correction for the NISQ hardware being deployed today, so let’s take a look at the basic schemes to correct single-qubit errors. But first, let’s look at the idea of using parity bits to correct errors in classical computers.

Here is the basic single-bit error correcting scheme based on the work of Richard Hamming. The basic variation of a hamming code from 1950, as shown below, is to use three parity bits to detect errors in four data bits.

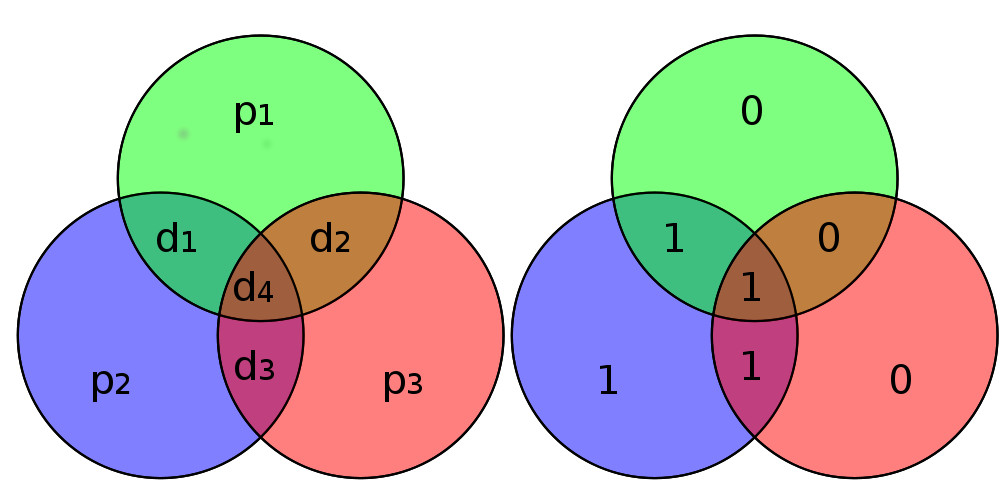
The bits labelled d1-d4 are the data bits, and p1-p3 are the parity bits used to do the error detection. The idea is to use the parity bits so that the sum from any one of the three circles will always be an even number. So for example, if d1=0, d4=1, and d3=1 then p2 would need to be zero, so 0+1+1+0 is an even number. If two of the circles adds up to an odd number, then the error is in the bit they have in common, and if all three circles add up to odd numbers then the error is in d4.

Note that this strategy requires three parity bits to detect a single bit error in one of the four data bits. If there are two bit errors we get unpredictable results. In classical computers the hardware is reliable so this is not problematic, but today’s NISQ quantum computers are not reliable enough to have this level of confidence.

A quantum hardware-based error correction scheme that is similar in design to the basic hamming codes is called a Steane Code. We’er still trying to detect single bit errors but there are now two types. Bit flip errors are errors in the value like when an X gate is applied and does not correctly rotate the qubit about the Y-axis; i.e. a zero is actually a one. A phase flip error is an error in the amplitude, like what happens when a Y gate malfunctions and fails to rotate the qubit about the Z-axis.

Shown above is a screenshot from a QuTech professsor Barbara Terhal’s presentation, and it shows for each set of four qubits, we have two parity qubits, labelled ancilla bits. This scheme will allow us to fix an error in one of the seven data qubits and none in any of the six parity bits.

Obviously the problems with quantum error correction schemes are motivation for less eror-prone technologies like trapped ion platforms and the elusive topological qubits. However there are also efforts at IBM to use statistical methods to do some error correction in software that might prove effective as well. They carefully measure baseline error rates, then ramp up the error production to higher levels and measure. Armed with this data they are able to extrapolate down to no errors, and it has proven effective in some experiments.