Multiverse 2.357
paused to apply patchesI won’t pretend to understand the physics of quantum mechanics, it baffles me to be honest. I only know the words that the physics people use to describe what happens. My limited understanding of quantum computing comes purely from a computer science perspective, so that’s all I can try to share.
A quantum bit, or qubit, is conceptually just the particle-wave duality of matter at very small scales. That is to say that a particle does not exist as a tiny billiard ball at a specific place, but rather has a probabilistic existence as a waveform. That’s the case until it is interacted with, otherwise known as being observed, which causes the quantum information to be lost and the probabilistic set of possible values to collapse into a single value.
I’m not going to try to explain why that is, or what is really happening here, since it’s beyond my understanding. Instead, I want to look at just the basic math that we need to understand how the qubits are affected by our gate operations. So let’s stick to the math, and explain exactly what happened in our quantum entanglement program used in our previous posts.
In case you want to read the hands-on introductions, here are my earlier posts on getting started:
Intro to IBM Q Experience
Quantum Computing Intro using Qiskit
Running a Program on IBM’s Quantum Computers
I can’t explain how entanglement works from a physics perspective, but we can simply define what it means in terms of logic, just like we explain how conventional computer logic works. A classic AND gate takes two inputs and has one output, and a truth table will show all four possible cases. If you’re comfortable with this, you’ll be fine.
A classical bit holds a value that is either interpreted to be a 1 or a 0. Since a qubit should be considered as a vector, there are multiple ways to represent it. Using Dirac notation, a qubit can be written as |0⟩ or |1⟩ or a combination of both. To represent two qubits both with a value of zero, using Dirac notation, we would write it as |00⟩.
Matrix Multiplication
Each qubit in a circuit starts with an initial state of zero, which actually means that the real part is zero, and the imaginary part is zero. A qubit that is measured to be 1 has a real part that is 1 and an imaginary part that is 0. If we use a matrix representation to show a 0 and 1 values respectively, we do it like this:
A zero is represented as and a one asIn case you don’t remember how matrix multiplication works, or you never learned it you multiply across in the first matrix and down in the second matrix, like so:
Notice in the example on the right, the result is identical to the right hand operand. The four by four matrix on the left is called the identity matrix for this reason. This matrix, with ones striped down the top left to bottom right diagonal is how the Identity Gate is represented.
Tensor Products
Multiple qubits are represented as tensor products. Transitive and associative properties hold here. A tensor product of vectors looks like this:
Are you still with me? This is all the math we need to make sense out of our qubits and gates! Now to tie it all together, let’s look at all four possible states of a 2-qubit circuit:
So we have three ways to represent our 2-qubit circuit shown above: Dirac notation on the left, a tensor product in the middle, and the individual state representation on the right.
We’ve actually seen a fourth way to represent qubits, called a Bloch sphere. That sphere with three axes is a great visual way to show qubits, but does not scale. A qubit starts at the north pole (|0⟩) and if we apply a Hadamard gate (superposition) we put it in the middle, on the surface of the sphere.
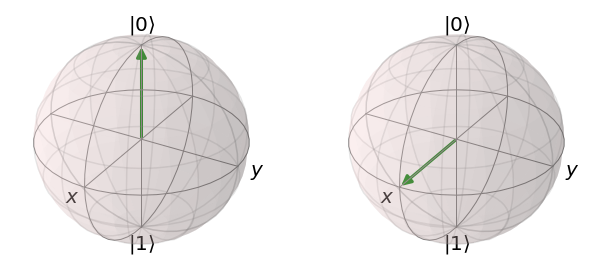
Above is shown the intial state of a qubit |0⟩ on the left. On the right is the same qubit after the Hadamard gate has been applied, which rotates it about the Y-axis to the equator. This is a nice visual way of showing what happened in the first step of our quantum entanglement program.
A standard measure operation measures it on the Z axis, which is the vertical line through the center of the sphere. This collapses X and Y to zero, and we measure the resulting value to be a scalar value interpreted as a zero or one, on one of the poles. Don’t worry if I explained it poorly, we’re going to stick to the math.
Controlled NOT Gate (CNOT)
We saw how the identity gate works using matrix multiplication earlier but honestly that’s a trivial case. So let’s return to our entanglement example, where the controlled not gate (CNOT) put two qubits into a state of entanglement. Recall that our control qubit q0 was first put in a state of superposition by application of a Hadamard gate, then the target qubit q1 gets involved as both are put in a state of entanglement by applying a CNOT(q0, q1).
Our CNOT gate can be represented as a matrix just like others, and applied to qubits. Remember if the control qubit is 1 the target qubit is flipped, otherwise not.
As expected, in the two cases where the control qubit (the first one) is a 0, the target qubit is not changed, and in the two cases where the control qubit is 1 the target qubit is flipped.
Summary
A few important things from this post are worth repeating. First, we can reduce what is happening to math without understanding the physics. Bloch spheres are a great way to visualize qubits, and since qubits are vectors we can also use dirac notation to represent them. Multiple qubits can be represented as tensor products. Also gate operations on qubits are represented as matrix operations, including gates that act on a single qubit and ones that act on multiple qubits.
So we have now covered one of the two gates used in our quantum entanglement program, and we’ll take a look at the Hadamard gate in the next post.